Úvod
Resonance je poměrně běžný jev, který se vyskytuje v řadě situací. Může jít například o resonanci mechanickou či o rezonanci při interakci elektromagnetických vln s hmotou nebo o resonanci u elektrických obvodů.
K resonanci může dojít na jedné či více frekvencích. Chování fyzikálních systémů se ve stavu resonance zpravidla výrazně liší od chování ve stavu mimo resonanci. Na rezonančních frekvencích mohou vznikat vlastní kmity systému. Obecně lze říci, že odezva výstupu na vstup je u fyzikálních systémů výrazně větší při resonanci než mimo resonanci.
Resonance je základem mnoha citlivých a přesných měřicích metod (NMR, EPR, RMA a mnoho dalších), resonance je také základem antén v elektronice atd. Mechanická resonance je i základem řády hudebních nástrojů. S mechanickou resonancí jsou také spojena s nebezpečnými jevy, jako je rozkmitání mechanických soustav.
Teorie mechanické resonance
Mechanická resonance jednoduchých elastických systémů
Nejprve se budeme zabývat jednoduchým mechanickým oscilátorem (obr. 1), tvořeným elastickým prvkem (pružinou) a setrvačným tělesem (závažím).
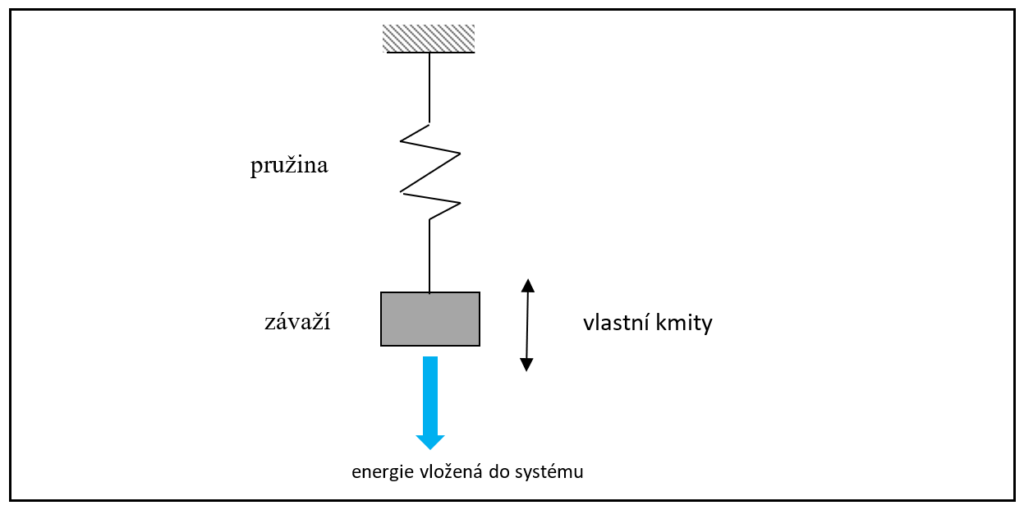
Obr. 1 Jednoduchý mechanický oscilátor
Rovnováha sil:
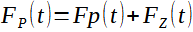
(1)
Předpokládejme, že energie se vnese do systému krátkým jednorázovým impulsem vnější síly (F). Tato síla je rovna součtu elastické síly v pružině (FP) a síly setrvačné (FZ).
Při dynamickém zatěžování dostáváme pro mechanické chování jednoduchou lineární diferenciální rovnici s konstantními koeficienty:
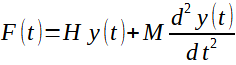
(2)
kde M je hmotnost závaží, y je deformace pružiny, H je tuhost (konstanta) pružiny.
Při aplikaci tohoto modelu na elastická tělesa předpokládáme, že celé těleso je možno považovat za složené z dvou členů, do kterých jsou soustředěny relevantní mechanické vlastnosti. Elastické vlastnosti jsou soustředěny do pružiny (nazývané obecněji Hookeovo těleso) a setrvačné vlastnosti do závaží (nazývané obecněji setrvačné těleso). Pružina má nulovou setrvačnost a závaží má nulovou deformaci.
Vlastní kmity
Přehledné a jednoduché řešení spočívá v aplikaci Laplaceovy transformace (dále L transformace) na rovnici (2). Dostáváme tak algebraickou rovnici:
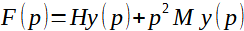
(3)
kde p je nová proměnná (místo času t).
Jednorázové vnesení energie do systému je ekvivalentní působení impulsu síly o velikosti A. V L transformaci pak platí:
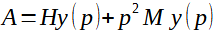
(4)
Pro další zjednodušení nebudeme v L transformaci proměnnou p označovat.
Pro y dostáváme:
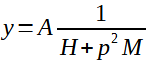
(5)
Vlastní kmity nastávají, je.li jmenovatel v rovnici (5) roven nule,
Jmenovatel rovnice (5) má kořeny:
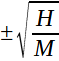
Z teorie L transformace plyne, že y v časové oblastimá průběh mají průběh:
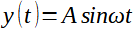
(6)
kde
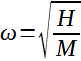
(7)
Podle stejných vztahů se řídí i mechanické oscilátory tvořené i jinými elastickými systémy, například elastickou tyčí. A to i pro další typy namáhání. Například pro namáhání v ohybu či torzi.
V praxi může setrvačný člen představovat i vlastní hmotnost tyče, je však třeba brát v úvahu, že setrvačná síla působí v tomto případě v těžišti tyče, na rozdíl od situace na obr 1, kde setrvačná síla působí na konci pružiny.
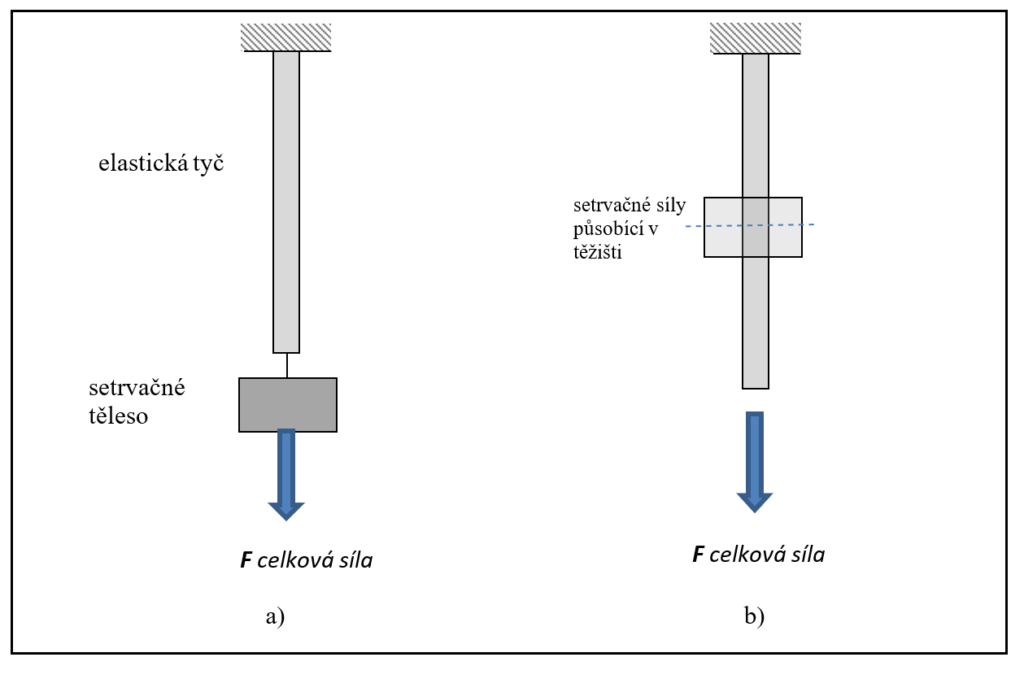
Obr. 2 Elastický tyč se setrvačným tělesem jako mechanický oscilátor při namáhání v tahu (a), elastická tyč bez setrvačného členu
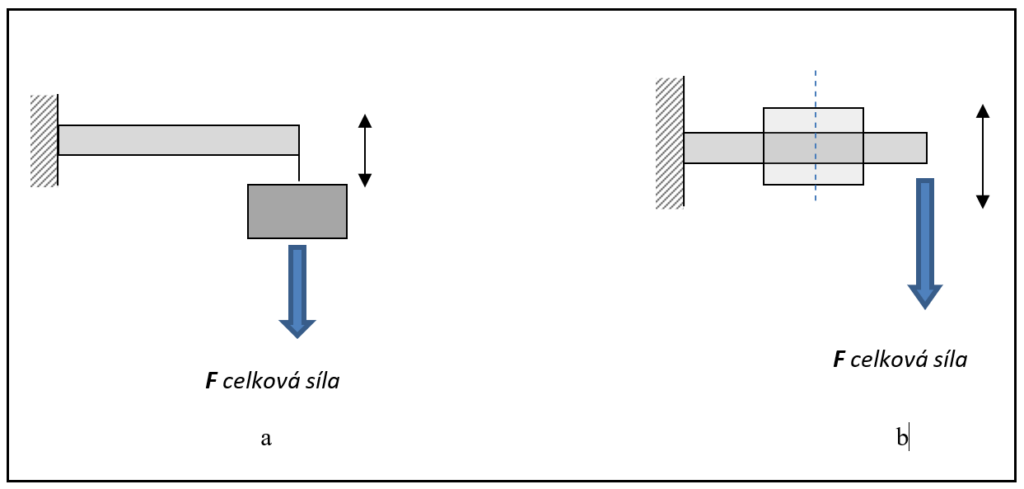
Obr. 3 Elastický tyč se setrvačným tělesem jako mechanický oscilátor při namáhání v ohybu (a), elastická tyč bez setrvačného členu
Resonanční křivky
Resonanční křivky vycházejí z frekvenční charakteristiky systému. Při resonanční frekvenci by amplitudy vibrací měly podle definice dosahovat maxima. Odvodíme vztahy pro maxima vibrací při konstantním buzení harmonickou budící silou.
Frekvenčních lze získat tak, že na základní diferenciální rovnici (2) aplikujeme Fourierovu transformaci. Dostáváme:
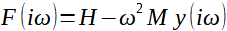
(8)
Pokud má budící síla F harmonický průběh, mají u lineárních systémů (náš případ) harmonický průběh i deformace y. Průběhy F(iω) a y(iω) se v tomto případě nazývají fázory (viz Dodatek).
Poměr fázorů:
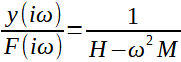
(9)
představuje frekvenční charakteristiku systému.
Frekvenční charakteristika je průběh harmonické odezvy při jednotkové amplitudě budící harmonické síly.
U elastických systémů dosahuje funkce (9) maxima (teoreticky jde k nekonečnu) při
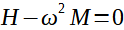
(10)
Resonanční frekvence odpovídá vztahu (7).
Poznámka: U složitějších elastických a viskoelastických systémů je situace složitější. Resonance může nastávat při více frekvencích..
Prakticky je důležité, jak rychle roste amplituda deformací v okolí resonanční frekvence. Příklad na obr. 4.
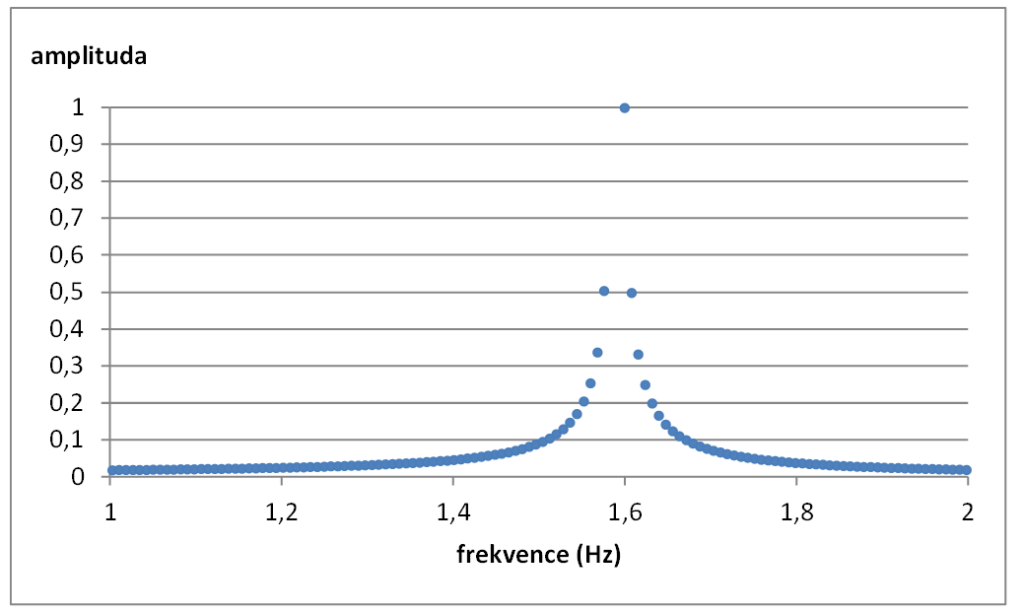
Obr 4. Příklad průběhu resonanční křivky (netlumeného) mechanického oscilátoru pro parametry pro parametry H= 100 N/m, M= 1kg
Mechanická resonance jednoduchých viskoelastických systémů
Nejprve se budeme zabývat jednoduchým tlumeným mechanickým oscilátorem (obr. 5), tvořeným elastickým prvkem (pružinou), setrvačným tělesem (závažím) a tlumičem.
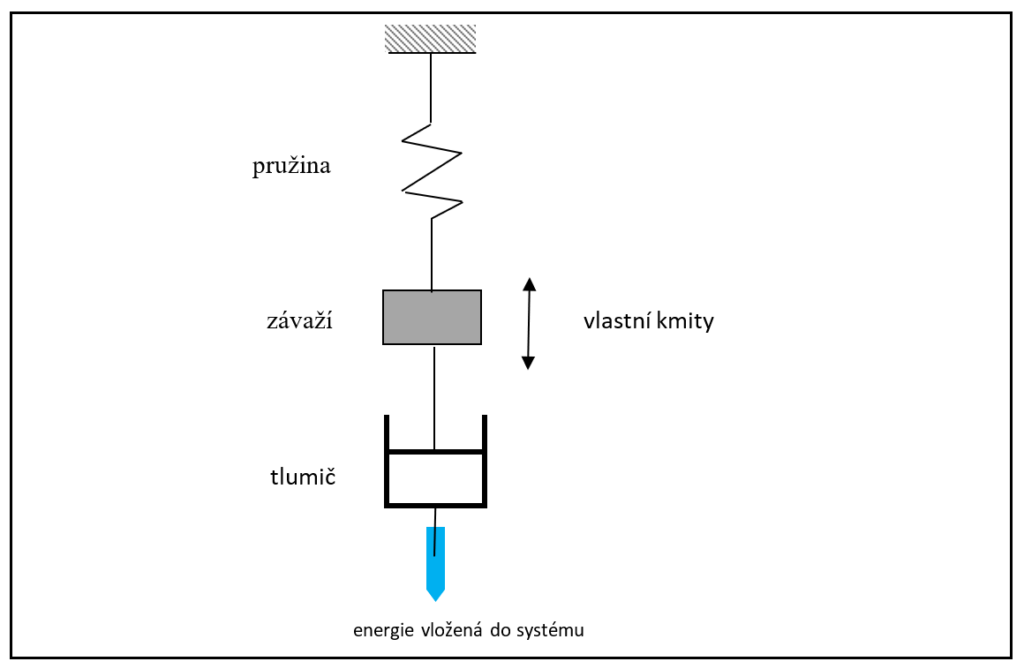
Obr. 5 Jednoduchý tlumený mechanický oscilátor
Rovnováha sil:
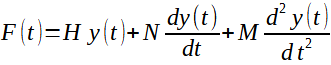
(11)
Předpokládejme, že energie se vnese do systému krátkým jednorázovým impulsem vnější síly (F). Tato síla je rovna součtu elastické síle v pružině (FP), síly setrvačné (FZ) a síly viskózní (FT) v tlumiči.
Při dynamickém zatěžování dostáváme jednoduchou lineární diferenciální rovnici s konstantními koeficienty:
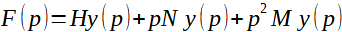
(12)
kde M je hmotnost tělesa, y je deformace pružiny, H je tuhost (konstanta) pružiny, N je koeficient tlumení (viskózní konstanta) tlumiče.
Vlastní kmity
Pro přehlednost a jednoduchost aplikujeme na rovnici (12) L transformaci. Dostáváme algebraickou rovnici:
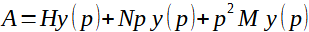
(13)
kde p je nová proměnná (místo času t).
Jednorázové vnesení energie do systému je ekvivalentní působení impulsu síly o velikosti A. V L transformaci pak platí:
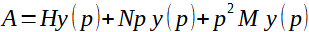
(14)
Pro další zjednodušení nebudeme opět v L transformaci proměnnou p označovat.

(15)
Kvadratická rovnice (15) má pro y v časové oblastiřešení:
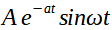
(16)
kde
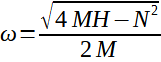
(17)
a
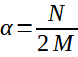
(18)
Podle stejných vztahů se řídí i tlumené mechanické oscilátory tvořené i jinými viskoelastickými prvky, například viskoelastickou tyčí. A to i dalších typů namáhání, kromě tahu. Například v ohybu či torzi.
Resonanční křivky
Při resonanční by amplitudy vibrací měly dosahovat maxima. Odvodíme vztahy pro maxima vibrací při konstantním buzení harmonickou budící silou.
Z hlediska přehlednosti je nejlépe vycházet z frekvenčních charakteristik. Tyto charakteristiky lze získat tak, že na základní diferenciální rovnici (12) aplikujeme Fourierovu transformaci.
Dostáváme:
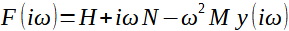
(19)
Pokud má budící síla F harmonický průběh, mají u lineárních systémů (náš případ) harmonický průběh i deformace y. Průběhy F(iω) a y(iω) se v tomto případě nazývají fázory.
Poměr fázorů:
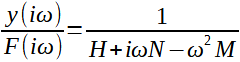
(20)
představuje frekvenční charakteristiku systému.
Tato frekvenční charakteristika je komplexní číslo. Skládá se z amplitudové a frekvenční charakteristiky.
Pro řešení podmínky resonance, podle definice resonance používané výše, je relevantní amplitudová frekvenční charakteristika. Jedná se o poměr amplitud deformace a amplitud síly v závislosti na frekvenci.

Resonance nastává, pokud výraz (22) dosahuje maxima. Tedy také
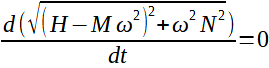
(23)
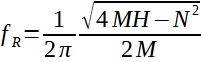
(24)
Tedy totožný se vztahem (17).
Zatímco u elastických systémů roste amplituda vibrací v resonanci teoreticky nad všechny meze, u viskoelastických systémů je omezena viskózní složkou. Pokud je amplituda budící síly jednotková, platí pro vibrace v resonanci vztah:
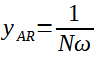
(25)
Prakticky je důležité, jak rychle roste amplituda deformací v okolí resonanční frekvence.
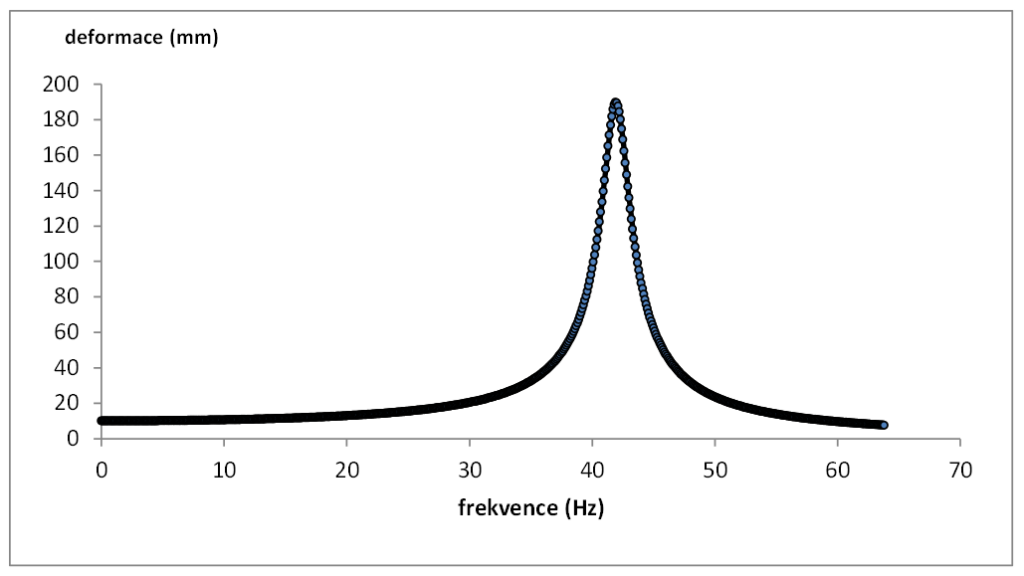
Obr 6. Příklad průběhu resonanční křivky v ohybu pro parametry: H= 100 N/m, N= 0,02 Ns/m, pro dřevěnou tyč 100x4x4 mm
Poznámka:
Z obr. 6 a také z použití vztahů (22) a (25) vidíme, že vibrace v oblasti resonance jsou obvykle 10 až 1000 větší, než vibrace mimo resonanci. Při měření pomocí resonanční metody (ve srovnání s přímým měřením resonanční křivky metodikou DMA) proto vystačíme s citlivostí snímaní podobně menší.
Mechanická resonance složitých viskoelastických systémů obecně
U jednoduchých elastických i viskoelastických systémů dochází k resonanci na jednom kmitočtu. U jednoduchých viskoelastických systémů dochází k resonanci pouze tehdy, pokud není viskózní
(tlumící) složka mechanického chování příliš vysoká. Podmínka resonance je: . Jinak systém nekmitá.
Avšak i u nekmitajících systémů lze však resonanci vyvolat přidáním dostatečně velkého vnějšího setrvačného členu.
U složitých viskoelastických systémů (například kompozitů či dřeva) může docházet k resonanci na více frekvencích. Resonanční křivka má v tomto případě více maxim. Důsledkem je, že vlastní kmity systému (po vnesení impulsu energie) nejsou tvořeny jednoduchou tlumenou harmonickou funkcí.
Resonance dlouhých tyčí a lan.
Úvod
Problematika vlastních kmitů dlouhých tyčí a lan má mimořádný význam v řadě oblastí, například ve stavebnictví. Mezi základní otázky patří frekvence a tlumení vlastních kmitů, průběhy deformace a namáhání podél těchto struktur či metodika eliminace vlastních kmitů. K řešení těchto problémů není možné jednoduše aplikovat metodiku uvedenou v předchozích částech této studie. Dlouhé struktury se totiž chovají jako systémy s principiálně rozloženými parametry. Teorie řešení mechanických systémů s rozloženými parametry není dosud uspokojivě vyřešena.
Cestu k praktickému řešení poskytuje analýza šíření mechanické vlny v těchto systémech.
Při řešení vyjdeme z rychlosti šíření mechanické vlny (určené experimentálně) a z odrazů vlny na okrajích tělesa. Interference přímé a odražení vlny umožňuje určit polohu maxim deformace a resonanční frekvenci.
Princip řešení pro rovnoměrnou tyč
Podél tyče se po vnesení energie krátkým impulsem šíří mechanické vlna. Pokud je tyč na konci pevně fixovaná, mechanická impedance pevného zakončení je mnohem vyšší než mechanické impedance tyče (teoreticky je nekonečná). V bodě pevného uchycení je nulová deformace a maximum namáhání. Pokud je zakončení tyče volné, je v místě zakončení maximální amplituda vibrací a minimální namáhání. Mechanická impedance volného konce má mechanickou impedanci mnohem nižší, než impedance tyče (teoreticky nulová).
V místech zakončení, pokud se impedance zakončení liší od impedance tyče, se vlna odráží. Interferencí přímé a odražené vlny vzniká stojaté vlnění.
Při vnesení energie krátkým impulsem se tyč samovolně rozkmitá takovými frekvencemi, kterým v místě pevného zakončení odpovídá kmitna namáhání (pokud je zakončení volné, v místě volného zakončení je naopak kmitna deformace). Na základě tohoto jevu lze určit rychlost šíření mechanické vlny a polohy případných dalších kmiten a uzlů.
Metodu lze použít i pro viskoelastickou tyč, pokud se v ní šíří mechanická vlna, tedy pokud viskózní složka není příliš vysoká.
Postup měření a výpočtů
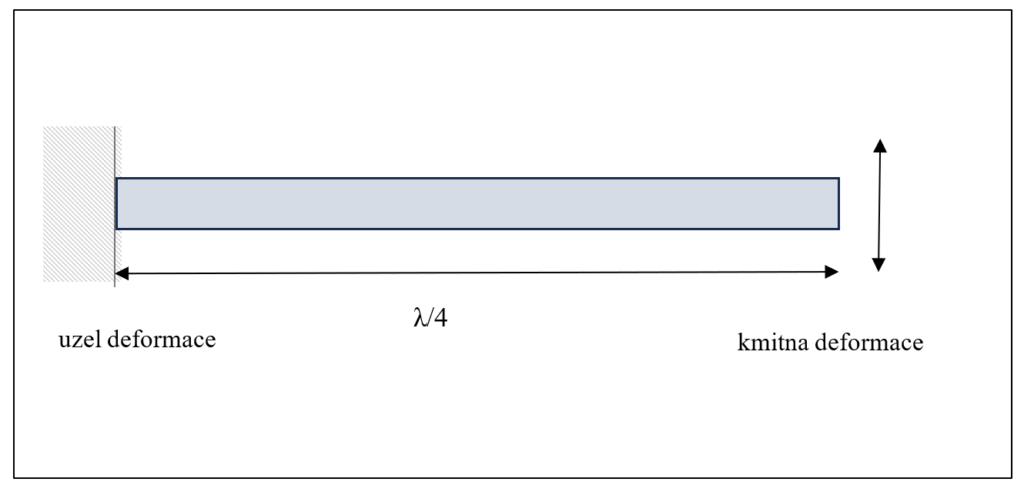
1) Změříme frekvenci f vlastních kmitů tyče o známé délce (obr. 7)
2) Protože délka tyče je λ/4, určíme rychlost v šíření mechanické vlny (není totožná s rychlosti šíření akustické vlny).
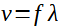
(26)
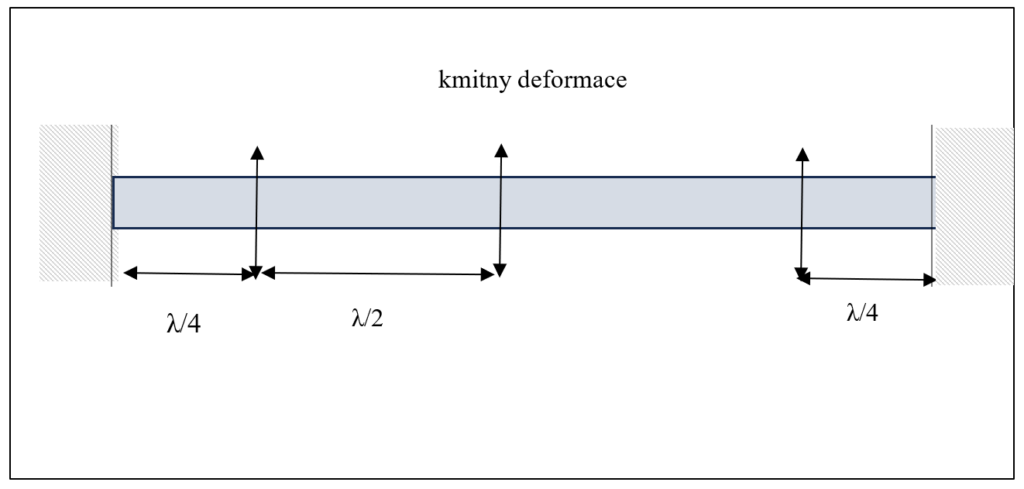
Obr. 8 Kmitání dlouhé tyče v ohybu, při pevném uchycení na obou koncích
Poznámka 1
Výše uvedená teorie je snadno aplikovatelná pro jednoosové namáhání.
Pro namáhání v 2D a 3D je aplikovatelnost obtížnější. Lze však poměrně snadno přejít od šíření vlny v jednom směru pomocí využití Huygensova principu a principu metody konečných prvků.
Převod mezi parametry tělesa a materiálovými konstantami materiálu u rovnoměrné tyče
Materiálové parametry jsou: Hustota ρ, modul pružnosti v tahu E, viskózní koeficient η.
Parametry tyče: jsou: Hmotnost M, tuhost H, Newtonův koeficient N.
Převodní vztahy:
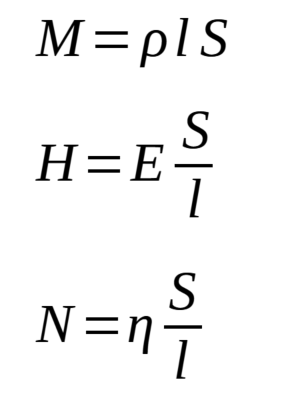
kde l je délka tyče, S je průřez tyče.